پارچه، در مقایسه با دیگر مواد مهندسی مرسوم و رایج در جهان، از نظر بسیاری از خصوصیات فیزیکی – مکانیکی متفاوت بوده و همین تفاوت، عامل کاربردهای منحصر به فرد آن گشته است. به عنوان نمونه، پارچه به دلیل شکل ساختار و نوع مواد تشکیل دهنده ی آن، قابلیت پذیرش تغییر شکل های مختلفی همچون: خمش، افتایش، چروک خوردگی و یا بادکردگی را بدون شکست و خرابی داراست؛ تغییر شکل هایی که در شرایط استفاده ی معمول – و به بیان دقیق تر مکانیکی: ” تحت تنش کم” – رخ می دهند و جابه جایی و کرنش در ساختار پارچه را به همراه دارند و همین ویژگی بی نظیر، کاربرد عظیم پارچه در زندگی انسان به نام ” پوشاک” را که پس از مسکن و خوراک، سومین نیاز اصلی بشر محسوب می شود به ارمغان آورده است.
نوشته ی حاضر، در خصوص یکی از همین تغییر شکل ها در پارچه به نام “برش” می باشد که در دیگر رفتارهای پارچه نیز به نوعی دخیل بوده و به اعتقاد نویسنده، اساسی ترین خصوصیت مکانیک پارچه قلمداد می گردد که می تواند روشن کننده ی خصوصیات اجرایی و عملی پارچه باشد.
برش چیست؟
در علم مکانیک، چهار نوع نیرو و تنش اصلی و در نتیجه آنها، چهار نوع تغییر فرم مختلف در اجسام، تعریف شده است که عبارتند از: کشش و فشردگی (Tensile & Compression)، خمش (Bending)، برش (Shear)و پیچش(Torsion). در این قسمت برای بررسی چیستی برش، این مفهوم ابتدا از نقطه نظر مکانیکی و سپس در مدیوم پارچه مورد بحث قرار می گیرد.
مفهوم برش از نقطه نظر مکانیکی
ماده ای به شکل مستطیل ABCD مفروض است (شکل ۱) به طوری که پایه ی آن یعنی ضلع CD ثابت می باشد و قابل حرکت نیست. تنشی به بزرگی F در طول ضلع AB اعمال می شود که در نتیجه ی این عمل، تنشی دقیقاً به همان اندازه در جهت عکس و در ضلع CD بروز می کند. هم اکنون یک جفت نیرو موجود است که مستطیل ABCD را به شکل جدید A1B1CD منحرف می کند. در اثر این تغییر شکل، زاویه ای نسبت به حالت اولیه (α) به وجود می آید که در واقع زاویه جابجایی در اثر اعمال نیرو است که با نام کرنش برشی (Shear Strain) شناخته می شود؛ و تنش برشی (Shear Stress) به صورت نیروی اعمالی بر واحد سطح AB یا (CD) تعریف می گردد. در صورت وجود الاستیسیته کافی در جسم، پس از حذف تنش، مستطیل به جایگاه اولیه خود باز می گردد. نسبت تنش برشی (نیرو بر واحد سطح) به کرنش برشی (جابجایی زاویه ای) با نام سختی یا مدول برشی (Rigidity or modulus of shear) شناخته می شود.

شکل ۱- ماده تحت تأثیر نیروی برشی [۲]
اگر تنش برشی افزایش یابد طول قطر مستطیل ABCD تغییر می کند. زمانی که طول BD تحت تنش کششی در حال افزایش است (Tensile stress)، طول ضلع AC کاهش می یابد؛ پس می توان نتیجه گرفت که تنش فشردگی (Compressive stress) در این جهت در حال اعمال است؛ در واقع این نیروهای داخلی پارچه هستند که با اثر جفت نیروی منحرف کننده مقابله می کنند و در نتیجه از تغییر فرم کامل و متلاشی شدن جسم تحت تنش برشی، جلوگیری می نمایند. اما اگر تغییر فرم در حد خرابی(از هم گسیختگی) رخ داد، باید به این نکته توجه شود که به طور معمول این گونه خرابی، ناشی از شکاف یا شکست ایجاد شده در طول صفحه مسطح موازی ضلع AB می باشد و این موضوع باعث می شود که قسمت بالایی جسم، پیش از قسمت پائینی آن – تحت نیروی منحرف کننده – بلغزد. پس به طور کلی می توان اظهار داشت که برش(Shear) تغییر فرم ذوزنقه وار یا به طور دقیق تر حرکت نسبی عناصر یا اجزاء ساختمانی جسم می باشد، که این حرکت و انحراف، نتیجهی لغزش عناصر تشکیل دهنده روی یکدیگر و کنار یکدیگر است.
مفهوم برش در معماری پارچه
پدیده برش، یکی از وجوه مختلف تغییر شکل پارچه است که در سطح (in-plane) اتفاق می افتد؛ و همانند دیگر تغییر شکل های پارچه، مثل آویزش، چروک، تاخوردگی، خمش و … مرتبط با اصول زیبایی پارچه می باشد، این قابلیت پذیرش تغییر شکل برشی – یکی از توانایی های فوق العاده ی پارچه در قیاس با دیگر مواد جهان پیرامون است که این امکان را به پارچه می دهد که به عنوان پوشاک بر بدن انسان انطباق مناسب داشته باشد بدون آن که برای انسان ایجاد احساس ناراحتی کند. در واقع توانایی پارچه برای پذیرش تغییر شکل برشی، شکل دهنده ی اصلی خصوصیات ویژه آن است؛ به طوری که پارچه قادر است از حالت دوبعدی به فرم های سه بعدی پیچیده، ایفای نقش کند.
زمانی که پارچه مورد استفاده قرار می گیرد، تقریباً تمام تنش های اعمالی کوچک هستند (Low Stress). به عنوان مثال توقع و نیاز بشر از پوشاک، داشتن قابلیت مطابقت با تمام حرکات بدن البته بدون ایجاد ناراحتی است که محقق حوزه مکانیک پارچه، John Skelton [4]، از آن تحت اصطلاحی به نام Conformal fitting یا انطباق مناسب نام برده است.
همانطور که گفته شد در هنگام استفاده از پارچه، تنش های کوچکی به پارچه اعمال می شود که در نتیجه ی آنها – و بعضاً ترکیب آنها – پارچه تحت تغییر شکل های مختلف و پیچیده قرار می گیرد. در شکل ۲ نمایی از مدل شبکه ای پارچه (Trellis mode) قبل و بعد از تغییر فرم برشی، نشان داده شده است که γ زاویه برش و τمعرف نیروی برشی است.
از مدل مکانیکی شبکه ای پارچه این طور بر می آید که بعد از تغییر فرم برشی اولاً زاویه نقاط تقاطع بین نخهای تار و پود تغییر می کند و ثانیاً طول نخ های تار و پود اگر نیرویی غیر از نیروی برشی به پارچه اعمال نشود، ثابت می ماند و این در حالیست که مساحت کوچک تر می شود و همین عامل است که باعث می شود پارچه، قابلیت پوشش سطوح انحنادار (Curved Surface) را بدون بادکردگی (Buckling) داشته باشد. کوچک شدن مساحت همان طور که در شکل پیداست به دلیل تغییر طول نمونه پارچه از L به L-∆L می باشد.
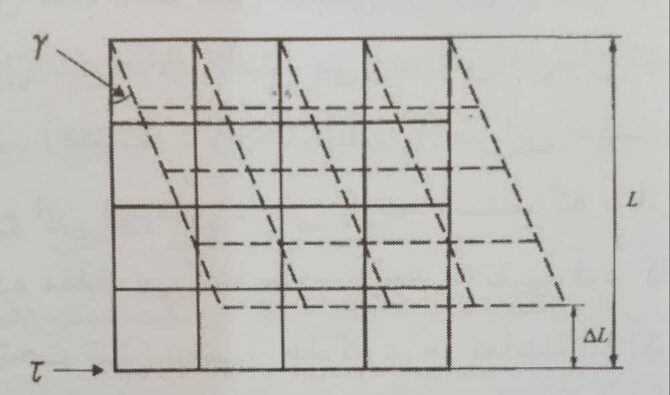
شکل ۲- مدل شبکه ای (Trellis Mode) تغییر فرم برشی در پارچه تاری پودی[۳]
می توان این واقعیت را اظهار داشت که تغییر شکل های نسبی پارچه در هنگام هر گونه استفاده که با تنش های کوچک ایجاد می شوند، تحت تأثیر خصوصیت انعطاف پذیری ساختمان پارچه می باشد. این تنش های کوچک سبب تغییر زاویه بین تار و پود شده که همان طور که پیش از این نیز ذکر شد این تغییر شکل زاویه ای به اصطلاح برش نام دارد. پس به طور کلی می توان این پدیده را در پارچه (تاری پودی) بدین صورت توضیح داد: برش، تغییر زاویه بین نخ های متقاطع است و هم چنین به عنوان نتیجه خمش و لغزش و تابیده شدن نخهای بین نقاط تقاطع نیز تعریف می شود. خواص پرشی پارچه از عوامل بسیار مهم و تأثیر گذار روی انعطاف پارچه، آویزش و خمش و زیر دست آن است که نه تنها برای منسوجات تاری پودی که برای انواع کامپوزیت ها و پارچه های لایه دار نیز از مسائل حائز اهمیت می باشد.
مکانیک برش در پارچه های تاری پودی
اگرچه در منظر اول و آن طور که پیش تر اشاره شد، برش مفهومی بسیار ساده دارد. اما در مطالعه جزئیات مکانیکی، بحث های پیچیده ای به وجود می آید. برای طرح مساله برش بهتر است ابتدا به ساکن کرنش برشی (shear strain)و پس از شرح آن، تنش برشی مورد بحث واقع شود.
کرنش برشی خالص عبارت است از تغییر شکل یک جسم به وسیله ازدیاد طول یکنواخت در یک جهت و انقباض در جهت عمود به آن که از این رو مساحت جسم ثابت باقی می ماند. نمای این نوع تغییر شکل در شکل ۳ آمده است.
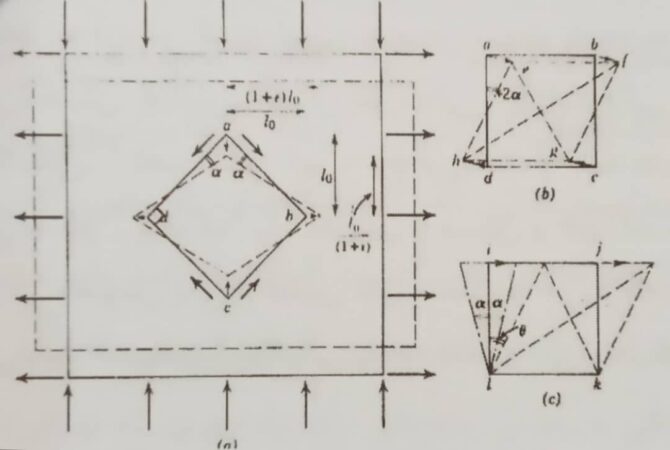
شکل ۳- (a) برش خالص (b) برش ساده (c) نمایه عمومی برش[۱]
اگر کرنش در یک جهت باعث ازدیاد طول به اندازه ی ε گردد طول خط۰ ε موازی با جهت ازدیاد طول، به مقدار (۱+ ε)L0 می رسد و از آنجا که مساحت ثابت است خط L0را در زاویه عمود به آن کاهش طول داده و طولش به مقدار (L0/(1+ ε)) می رسد. در جایی که کرنش کم باشد مورد اخیر مساوی با (۱- ε)L0 است که مقدار عددی کرنش برای ازدیاد طول و همچنین کاهش طول مساوی خواهد بود. با توجه به شکل، مشهود است که چهار گوش abcd با حالت اریب در جهت کرنش اصلی، تغییر شکل داده است. ولی مساحت آن تغییر نکرده، بنابراین اضلاع آن نسبت به حالت قبل دارای زاویه α خواهند بود؛ و زوایا در گوشه ها به اندازه ۲α از مقدار π/۲ (یعنی به مقدار(π/۲±۲α )) تغییر نموده اند.
باتوجه به قضیه فیثاغورث می توان بیان نمود که اضلاع چهار ضلعی abcd به اندازه [۱/۲{(۱+ ε)۲+(۱+ ε)-۲}]۱/۲ طولشان اضافه شده است. حال اگر چهار گوش abcd را بچرخانیم به طوری که یکی از اضلاع، موازی جهت اصلی قرار گیرد، نمایه ی کرنش برشی ساده آن مطابق شکل (.b3) است. جابجایی واقعی یا برش گوشه های چهار ضلعی در جهت های ae، bf، cg و dh می باشد که موازی یکدیگرند. با این تفاسیر اگر یک چهار وجهی در نظر گرفته شود که گوشه های آن به یکدیگر عمود و موازی با جهت برش ساده باشند، بعد از اعمال برش شکل آن مطابق شکل (.c3) خواهد بود که این تغییر شکل در واقع ایده اولیه برش است که اضلاع آن در جهت عمودی با زاویه θ هم جهت با برش، زاویه دار می گردند. مقدار کرنش برشی θ tan است.
بعد از ارائه یک نمایه از کرنش برشی، نوبت به تنش برشی می رسد؛ تنش برشی عبارت است از نیروی وارده به صورت تانژانتی به صفحه (یا در طول یک خط اگر با صفحه های دو بعدی مواجه باشیم)؛ البته این پدیده به صورت متوازن انجام می شود، یعنی نیرویی در جهت مخالف و در یک صفحه با آن وجود دارد تا نیروی گشتاور ثانویه حاصل از آن، از چرخش جلوگیری نماید.
بعد از این توضیح، واکنش ناشی از اعمال تنش برشی به یک نمونه پارچه مورد بررسی قرار می گیرد؛ در حالت کلی تغییر شکل های پیچیده ای ناشی از بردارهای تنش ایجاد می گردد که مهم ترین مساله، تغییر شکل در جهت تنش برشی است که به آن کرنش برشی (tanθ) گفته می شود و ارتباط بین این دو فاکتور منحنی تنش – کرنش می باشد. این تنش سبب می شود نمونه بصورت آزاد برش پیدا نماید و بعد دیگر آن به شکل دلخواه تنظیم شود.
در شکل (.a3) تعادل برش خالص که ترکیب تنش کششی مثبت و منفی در جهت های عمود به یکدیگر می باشد نشان داده شده است اما برای حالت های دیگر تغییر شکل برشی، دارای توزیع کرنش کششی دقیقاً یکسان و همگون نیست بلکه سبب ازدیاد طول در bd و فشردگی در طول ac می شود. اما نکته بسیار مهم و قابل توجه این است که همراه با این کرنش، تنش نیز وجود دارد و این موضوع موجب یک مشکل حقیقی می شود: پارچه، ورقه نازکی است که در آن تنش فشردگی نمی تواند ایجاد شود مگر این که به راحتی بادکردگی (buckling) به وجود آید.
بسیاری از محققین و متخصصین نساجی، در پی مطالعات پیرامون پدیده برش بر این باورند که بادکردگی یا buckle در حین عمل برش، تقریباً بزرگ ترین مشکل برای طراحی یک دستگاه آزمایشگر ایده آل می باشد.
به طور کلی می توان اظهار نمود که اندازه گیری برش و تورم پارچه (بادکردگی) و کلیه ی موادی که به شکل ورقه ای می باشند و سختی کششی و سختی خمشی آن ها بسیار پائین است – به راحتی کشیده یا به راحتی خم می شوند – نیازمند دستگاههای با دقت بالا می باشد.
مدال مکانیکی برای تشریح رفتار برشی پارچه
شکل ۴ نشان دهنده ی یک مدل رئولوژیک مکانیکی است که برای تشریح و توصیف رفتار اصلی حرکت برشی در پارچه های تاری پودی مطرح شده است. همان طور که مشاهده می شود این مدل دارای یک المان اصطکاکی و دو المان الاستیکی است. همچنین شکل ۵ منحنی نیرو- تغییر شکل حاصل از این مدل را نشان می دهد.
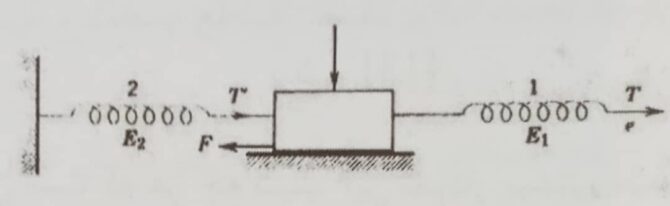
شکل ۴- مدل رئولوژیک برای تشریح رفتار برشی پارچه [۱]
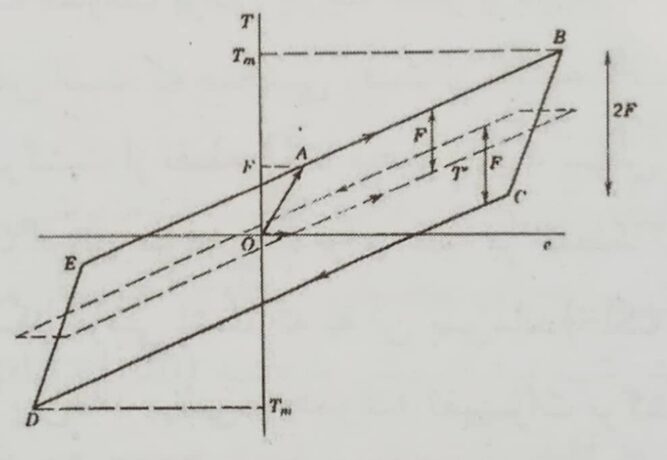
شکل ۵- منحنی حاصل از مدل رئولوژیک برای تشریح رفتار برش پارچه [۱]
شروع از حالت استراحت با نیروی کششی صفر وارد به هر دو فنر بوده، حرکت با اعمال نیروی T می باشد که باعث ازدیاد طول فنر ۱ است؛ این حرکت اولیه در نمودار حاصله، یا خط OA و با مدول E1 مشخص است. در واقع این مرحله شروع برشی می باشد که در نقاط تقاطع نخها، هیچ گونه حرکت یا لغزشی پیش نیامده، ولی نخ های بین این نقاط تقاطع کمی جابجا می شوند. زمانی که نیروی T به مقدار لازم برای غلبه بر نیروی اصطکاکی قطعه اصطکاکی (بلوک) می رسد، لغزش نخ ها در نقاط تقاطع شروع می شود وازدیاد طول بیشتر، از این به بعد بین فنرهای ۱ و ۲ تقسیم می گردد. خط AB در منحنی نیرو- تغییر شکل، نمایانگر تغییر شکل دو فنر می باشد که به صورت سری با هم بسته شده و مدول آنها از رابطه (۱) محاسبه می شود.
E1E2/((E1+E2))رابطه (۱)
توصیف این حالت در پارچه قابل تأمل است؛ با این توضیح که در واقع پارچه هم در نخ های بین نقاط تقاطع و هم در نقاط تقاطع اش دارای مساله ی برش شده است، در این مرحله مقاومت الاستیک در نقاط تقاطع وجود دارد.
حال فرض بر این است که در این لحظه، حرکت برعکس شده، یعنی برش پارچه تا نقطه B روی منحنی، در جایی که نیرو Tm است، متوقف شده و برگشت می نماید (Recovery). این برگشت ابتدا به ساکن تنها در فنر ۱ صورت می پذیرد، زیرا نیروی اصطکاک از حرکت بلوک جلوگیری می نماید. این ناحیه بازگشت، در نمودار به صورت خط BC موازی OA نمود دارد. در این منطقه، نیروی کشش در فنر ۲ دارای مقدار ثابت (Tm-F) است، اما زمانی که نیروی T به مقدار (Tm-2F)کاهش می یابد، این مقدار جهت لغزش بلوک به سمت عقب کافی خواهد بود. خط CD در نمودار موازی با AB تا کشش -Tm در نقطه D ادامه یافته و مسیر همانند قبل تکرار شده و حلقه BCDE بسته می شود و سیکل یک حرکت برشی از مرحله شروع تا برش نهایی در نیروی کشش Tm و سپس بازگشت تا نقطه شروع و ادامه حرکت در جهت عکس برش تا رسیدن به نیروی کشش Tm و دوباره بازگشت آن تا شروع حرکت برش، کامل می شود.
در این منحنی سه مرحله اصلی مهم و قابل توجه است و مابقی آنها تکرار شده است. شروع حرکت یعنی نقطه O می باشد که هنوز هیچ حرکتی وجود ندارد. منطقه OA که حرکت برشی در نخ های بین نقاط تقاطع دیده می شود ولی هنوز لغزشی در نقاط تقاطع دیده نمی شود. منطقه AB که در خود نقاط تقاطع لغزش وجود دارد و در واقع مقدار انرژی برای غلبه بر نیروهای اصطکاکی صرف شده است.
ارزیابی خصوصیت برشی
امروزه پیشرفت های قابل ملاحظه ای در زمینه های مختلف علوم مهندسی تکنولوژی نساجی، با به کارگیری فن آوری های مدرن حاصل شده است. ماشین آلاتی با سرعت تولید و کیفیت بالا در زمینه تولید نخ پارچه و تکمیل آن بوجود آمده اند که نسبت به دوره های قبل از دقت بسیار بالاتری برخوردار می باشند. همگام با این جهش های صنعتی مسأله ی کیفیت سنجی که به لحاظ علمی مربوط به تشخیص ذاتی میباشد، نمود بیشتری یافته و با تحقیقات به عمل آمده، تبدیل به خصوصیتی قابل اندازه گیری شده است.
دستگاه آزمایشگر معتبری که هم اکنون برای ارزیابی خصوصیات کششی، برشی، خمشی و فشردگی پارچه به عنوان روش پیشرو محسوب می شود، دستگاه آزمایشگر (Kawabata Evaluation System) KES می باشد. همان طور که پیشتر نیز اشاره شد، شیوع بادکردگی در پارچه شکل اصلی برای ارزیابی خصوصیت برشی است، که دستگاه KES، با الحاق یک کشش یکنواخت به سمت ثابت نمونه ی در حال تغییر فرم، تا حد زیادی بر این تورم و بادکردگی غلبه کرده است.
روش معتبر دیگری که در بسیاری از منابع علمی و مقالات تحقیقی، از آن برای تعیین خصوصیات برشی پارچه تاری پودی نام برده و استفاده شده، روش آزمایش کششی در جهت °۴۵ (Bias extension) پارچه می باشد.
استحکام سنجی در راستای اریب (۴۵ درجه)
این روش مبنای کار در سیستم اندازه گیری زیر دست پارچه به نام (Fabric Assurance by Simple Testing) FAST می باشد که ابزاری بسیار ساده برای اندازه گیری خواص مکانیکی پارچه بوده و کاربرد صنعتی دارد. وقتی پارچه در زاویه ۴۵ درجه نسبت به تار، تحت نیروی کششی قرار می گیرد، نخ های تار و پود حرکتی کاملاً قیچی گون دارند و جابجایی نقاط تقاطع و زوایای آنها بیشتر از هر حالت دیگری از آزمایش کشش است و طبق تعاریف فصل یاد شده در همین مقاله، می دانیم که مقاومت نخ های بافت پارچه، در برابر تغییر زوایای نقاط تقاطعشان، مقاومت برشی است. بر این مبنا، مقاومت کششی پارچه در زاویه ۴۵ درجه، همان مقاومت برشی است، نمودار حاصل از این آزمایش در شکل ۶ مشهود است. ناحیه اول، برش اولیه است، یعنی زمانی که زاویه ی بین نخها در قسمت مرکزی نمونه شروع به تغییر می کند. انتهای ناحیه اول، نقطه بحرانی است که زاویه برش بحرانی حاصل شده است و در واقع نخ های ناحیه مرکزی نمونه، حالت فشردگی پیدا می کنند. در این مرحله بحرانی، افزایش تنش باعث افزایش فشردگی نخهای پهلویی شده و این آغاز موج بادکردگی می باشد
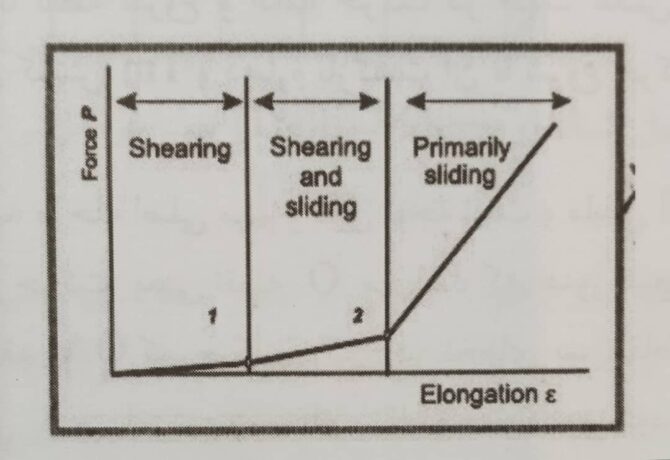
شکل ۶- نمودار استحکام در نمونه بریده شده در جهت اریب [۱۰]
ناحیه ۲، از لغزش نقاط تقاطع شروع می شود، یعنی تغییر مکان آنها. نقطه انتهایی این مرحله، محدوده ی قفل شدن زاویه برش است (Locking shearing angle) و نخها تحت تغییر فرم برش (کشش بیشتر) نمی توانند جابجایی داشته باشند. در مرحله سوم، فشردگی نخ های پهلویی کاسته شده است، و این یعنی سطح پارچه تدریجاً خم شده و پارچه شروع به چروک . خوردگی می کند و این یعنی تغییر فرم برش، تمام شده است.
به طور کلی این روش آزمایش بسیار ساده عمل نموده، با ارزیابی میزان تغییرات طول در زاویه اریب، مقاومت برشی پارچه را می سجند. در قسمت بعد، چگونگی تحلیل منحنی برش پارچه به طور کامل تشریح و در ادامه، دیگر دستگاه آزمایشگر برش پارچه مطرح می گردد.
تشریح منحنی برش پارچه
از آنچه تاکنون درباره برش یاد شد، می توان دریافت که برشی در پارچه های تاری – پودی، در اثر حرکت نسبی دو دسته نخ تشکیل دهنده پارچه، یعنی تار و پود ناشی می شود، نخ هایی که به صورت متقاطع در هم بافته شده اند تا پارچه به وجود آید. رفتار برشی پارچه تاری پودی توسط نمودار تنش کرنش حاصله، تا حد خیلی دقیقی قابل مشاهده است. همان طور که در شکل ۷ دیده می شود اگر پارچه با ازدیاد طول کوچکی تغییر شکل داده شود – یعنی ناحیه OA – سختی برش در ابتدا بسیار بزرگ است. با افزایش کرنش، این مقدار افزایش می یابد. در این ناحیه مکانیزم های اصطکاکی بر رفتار برش چیره است و کاهش شیب نمودار مربوط به تحرک مداوم عناصر اصطکاکی است. به محض این که تنش برای غلبه بر نیروی اصطکاک به اندازه کافی بزرگ شد – نیروی اصطکاکی که در نواحی تقاطع نخ های پارچه وجود دارد – سیستم شروع به لغزش می کند و سختی موجود در پارچه افت پیدا می کند، این ناحیه AB می باشد. در ناحیه ای مخصوص از تنش، سختی به پائین ترین حد خود یعی نقطه B می رسد و اثرات باقیمانده که به طور تقریبی خطی هستند با شیب به پایان محدوده می رسند که گمان می رود این شیب تحت کنترل تغییر شکلی در پارچه به نام “عناصر الاستیکی” در پارچه می باشد.
در دامنه های بزرگتر، یعنی نقطه C سختی دوباره شروع به افزایش می کند. به نظر می رسد که این مورد تحت تأثیر دو خمیدگی نخهای متقاطع در پارچه یا روی هم سوار شدن نقاط تقاطع، یا هر دوی آنهاست.
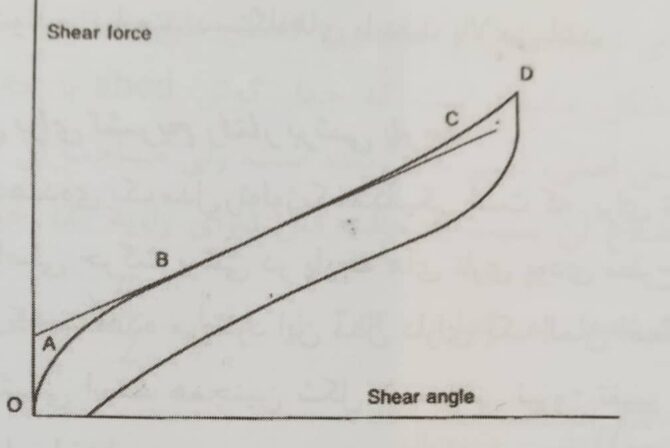
شکل ۷- منحنی تنش- کرنش پارچه های تاری – پودی در حین تغییر شکل برشی [۱۳]
واضح و مبرهن است که هر چه شیب این نمودار بیشتر باشد. در واقع کمیت مقاومت برشی بیشتر بوده و پارچه شق تر و سفت تر است و هر چه این شیب به افق نزدیک تر باشد، مقاومت برشی پارچه کمتر و پارچه لخت تر است.
طبق نمودار مشخص است که منحنی رفت از نقطه A تا D، دارای تفاوت فضایی با منحنی برگشت از نقطه D تا محور زاویه برش (افقی) است. این تغییر فضایی معرف انرژی صرف شده برای غلبه بر اصطکاک بین نقاط تقاطع نخ ها برای تغییر شکل برشی است که به آن پس ماند(Hysteresis) گفته میشود. پس در واقع پس ماند برشی، مجموعه تغییرات برگشت ناپذیر در طی فرآیند برش پارچه است که مقدار آن با محاسبه مساحت بین دو منحنی حاصل می گردد.
سیستم ارزیابی کاواباتا (KES)
دستگاه آزمایشگر KES از دیر باز – ۱۹۷۲، سال اختراع آن – مورد توجه کترشناسان و متخصصین کیفیت شناسی پارچه بوده است و برای مصارف مختلفی چون ارزیابی قابلیت دوخت پارچه یا زیر دست آن، به کار می رود و هم اکنون روش پیشرو و در واقع روش مرجع برای ارزیابی خصوصیات برشی شناخته می شود.
شماتیک این دستگاه در شکل ۸ آمده است. قابل توجه است که این دستگاه خصوصیات برشی و همچنین کششی پارچه را ارزیابی می نماید.
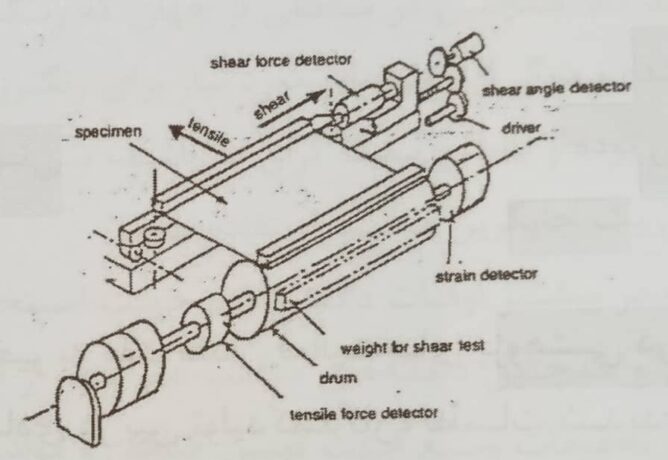
شکل ۸- شماتیک دستگاه آزمایشگر KES برای ارزیابی خصوصیات برشی و کششی پارچه [۱۷]
از منحنی حاصل از آزمایش برشی KES (مشابه شکل ۴) دو پارامتر اصلی نتیجه می شود:
۱- سختی برشیG: که به عنوان شیب میانگین منحنی تعریف می شود و واحد آن gf/(Cm.degree) می باشد.
۲- پس ماند: که دو مقدار دارد و با عناوینHG ۲ و ۵HG۲ مشخص می گردد. این مقادیر نشان دهنده ی عرض منطقه ی پس ماند برای زوایای برش °۵/۰ = φ و °۵ = φ می باشند.
جمع بندی
از آن چه سخن رفت می توان به نکاتی کلیدی و مهم به عنوان جمع بندی نهایی اشاره نمود:
– رفتار برشی پارچه تاری پودی را می توان طی ۴ مرحله اصلی، طبقه بندی نمود:
الف. تغییر شکل پارچه تحت تاثیر نقاط تقاطع سخت و غیر منعطف، زمانی که نیروی برشی بسیار کوچک است
ب. لغزش نخ ها در نقاط تقاطع، و در ادامه تغییر مکان تدریجی نقاط تقاطع نخ های تار و پود.
ج. تغییر شکل الاستیک، زمانی که لغزش کامل می شود و به حد نهایی خود می رسد.
د. فشرده شدن ساختمان پارچه.
– مقاومت بسیار اندک پارچه در برابر تغییر فرم برشی در مقایسه با تغییر فرم کششی، آن را برای پوشش سطوح انحنادار مناسب ساخته است؛ به طوری که کاربرد اصلی پارچه (Major application) یعنی پوشاک، توسط قابلیت برش پذیری میسر می شود. به بیان دیگر شرط لازم برای انطباق مناسب پارچه بر سطوح سه بعدی، پذیرش تغییر شکل برشی است و از این رو شناخت، تعیین پارامترهای اندازه گیری و چگونگی این رفتار تحت تاثیر تغییرات خصوصیات نخ و تنظیمات ساختار پارچه، برای مهندسان معمار پارچه بسیار مفید است.
منابع
References:
۱. Hearle, J.W.S., Grosberg. P. Backer, S. (1969), “Structural mechanics of fibers, yarns, and fabrics, Vol.1”. John Wiley & Sons, Inc.
۲. Slater, K. (1987). “Textile Mechanics, Vol.2”. First Published, Manchester: The Textile Institute.
۳. Zheng, J. et al. (2006). “Evaluating shear rigidity of woven fabrics Textile Res. J. 76, pp. 145-151.
۴. Skelton, J., (1976). “Fundamentals of fabrics to shear”. Textile Res. J.. 46, PP 862-869.
۵. Sun, H.. Pan. N. (2005). “Shear deformation analysis for woven fabrics”. Composite structure, 67, pp.317-322
۶. Kawabata, S. et al. (1970), “The finite-deformation theory of plainweave fabrics, Part III: The shear deformation theory”. J. Textile Inst. August 1970, pp. 62-85.
۷. Leaf, G.A.V., Sheta, M.F. (1984). “The initial shear modulus of plainwoven fabrics”, J. Textile. Inst., No.3, pp. 157-163.
۸. Cusick, G.E. (1961). “The resistance of fabrics to shearing forces”. J. Textile Ins., 52, T395-T406.
۹. Skelton, J., Freeston, W.D., (1971), “Mechanics of elastic performance of textile materials, Part XIX: The shear behavior of fabrics under biaxial loads”. Textile Res. J., 41, pp.871-880.
۱۰. Domskiene, J., Starzdiene. E..(2005). “Investigation of fabric shear behavior” Fibers & Textiles in Eastern Europe, 50, pp.26-30.
۱۱. Morner, B., Eeg-Olofsson, T., (1957). “Measurement of shearing properties of fabrics” Textile Res.J., 27. pp.611-615.
۱۲. Hu, J., (2004). “Structure and mechanics of woven fabrics”, first published, The Textile Institute, Wood head publishing Ltd and CRC Press LLC.
۱۳. Hu, J., Zheng, Y. T. (1997). “The KES shear test for fabrics”, Textile Res, J., 67, PP.654-664.
۱۴. Kilby, W.F. (1963). “Planar stress-strain relationships in woven fabrics”. J.Textile Inst., 54, T9-T27.
۱۵. Buckenham, P.. (1997). “Bias-extension measurements on woven fabrics”. J.Textile Ins., 88, p.p.33-40.
۱۶. Mario Bona, (1994), “Textile Quality, Physical method of product and process control”, TEX ILIA, Italy.

