فیلترهای بیبافت
بخش نهم- تئوری فیلتراسیون
دکترمیررضا طاهری اطاقسرا
عضو هیئت علمی دانشگاه صنعتی امیرکبیر (پلیتکنیک تهران)
در بخش هشتم از این مجموعه به چهارمین و آخرین تئوری از تئوریهای فیلتراسیون یعنی”جریان از میان لایه متخلخل” یا ” تئوری مدل سلولی” پرداخته شده است. در این بخش به ادامه این تئوری میپردازیم.
د) جریان از میان لایه متخلخل : تئوری مدل سلولی (ادامه)
۴- پیشرفتهایی در تئوری مدل سلولی
تئوری های ارائه شده به وسیله کوابارا و هپل چندین بار مورد بازنگری قرار گرفته و روز آمد شدهاند. پیچ (Pich) با فرض اینکه مقداری لغزش در سطح سیلندر داخلی وجود دارد مدل کوابارا را اصلاح کرد. معادله حاصل در عبارات بیبعد دیویس به صورت زیر است:
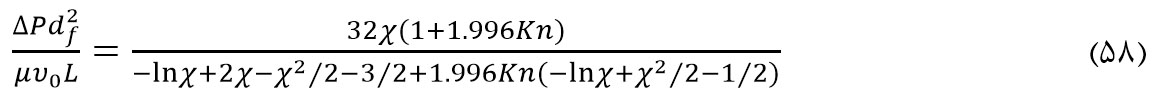 Kn عدد نودسن (Knudsen) است که به صورت زیر تعریف می شود:
Kn عدد نودسن (Knudsen) است که به صورت زیر تعریف می شود:
 بطوریکه:
بطوریکه:

پیچ ادعا کرده است که معادله او برای شرایطی که λ در مقایسه با قطر لیف df خیلی کوچک باشد صادق است. ناحیه قابل اجرا ناحیهای است با Kn<0.25. گراف (Grafe) و گراهام (Graham) اشاره کردهاند که در قطر های کوچک الیاف (۰.۵ μm ) جریان لغزشی باید در نظر گرفته شود.
براون اشاره می کند که قوت تئوری مدل سلولی در سادگی آن است. در این مدل فرض می شود که یافتن جریان هوا در اطراف یک لیف دوار تکی حکایت از کل فیلتر دارد. براون اشاره داشته است که در یک لایه واقعی نه تنها همه الیاف عمود بر جریان نیستند بلکه همهی آنها دارای قطر یکسان و یکنواخت نیستند. علاوه بر این مقطع عرضی الیاف لزوما دوار نیست. او همچنین اشاره کرده است که فشردگی در میان لایه متغیر است. براون اظهار می دارد که هیچ تئوریای وجود ندارد که این همه مسائل را در نظر بگیرد. با این حال بعضی اصلاحات و بهسازی در این امر وجود دارد. میاگی (Myagi ) رویکردی با یک متغیر پیچیده را برای عملکرد فیلتر به عنوان یک ردیف بیکران واحد از الیاف موازی با فضای مشابه استفاده کرده است. بر اساس نظریه براون این رویکرد نتایجی را ارائه میدهد که با تئوری سلولی قابل مقایسه است به شرط اینکه فاصله بین دو لایه مجاور از ردیفها برابر فاصله الیاف در داخل یک ردیف باشد.
کیرش و فاخس یک مدل پنکهای (fan model) را کشف کردهاند. این رویکرد شامل صفحههای متوالی از الیاف سلولزی می باشد، اما الیاف موجود در هر صفحه با زاویههای دلبخواه (دیمی) و با توجه به الیاف موازی در صفحات قبلی دوران میکردند. مدل پنکهای بر اساس پراکندگی همگن کامل از الیاف بود. در یک لایه فیلتر واقعی پراکندگی الیاف چندان همگن نیست. مدل پنکهای مقاومت بیشتری را نسبت به فیلترهای واقعی پیش بینی میکند. بنابراین، برای اینکه شرایط یک فیلتر واقعی به مدل پنکهای نزدیک شود، یک فاکتور ناهمگنی (inhomogeneity factor ) به وسیله فاخس و همکارانش معرفی ارائه شده است.
فرض اینکه فاصله بین لایههای یک فیلتر برابر است با فاصله الیاف در داخل لایه، الزاما صحیح نیست. در یک فیلتر عمقی (depth filter) ردیفهای متوالی الیاف موازی، سادهترین رویکرد برای ارائه یک مدل تئوری است. دو حالت از این ردیف ها در شکل ۱ نشان داده شده اند.
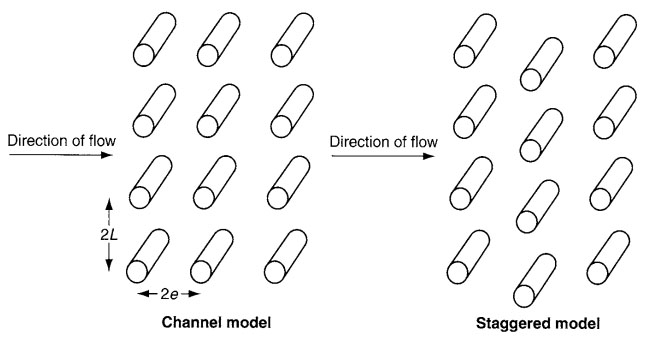
شکل۱- ردیف های الیاف موازی
در شکل ۱، سیلندرها (استوانه ها) بخشهایی از الیاف موازی که بر جهت جریان عمود هستند را نشان میدهند. هر ردیف عمودی از سیلندرها نشان دهنده یک لایه از لایههای فیلتر میباشد. مقدار ۲l عبارت است از فاصله بین الیاف موازی در داخل لایه. مقدار ۲e عبارت است از فاصله بین دو لایه. در شکل ۱ دوساختمان نشان داده شده است. در ساختمان کانالی فرض میشود که الیاف موجود در هر لایه مستقیما در پشت الیاف واقع در لایه جلویی خود صف کشیده اند. مدل متناوب (ضربدری) شیوهای را نشان میدهد که در آن ترتیب قرار گرفتن الیاف از یک لایه به لایه دیگر به صورت متناوب میباشد. براون چهار ساختمان را به تصویر کشیده است. این چهار ساختمان شامل ساختمان کانالی و سه نوع ساختمان متناوب است. پارامترهای این ساختمانها عبارتند از مقیاس (scale)،کسر تراکم (packing fraction) و نسبت فاصله لیف – لیف به فاصله لایه – لایه . اگر حالت متناوب بین لایه های متوالی وجود داشته باشد، آنگاه پارامتر چهارمی برای توصیف وجود حالت متناوب لازم است. براون چهار رویکرد زیر را پیشنهاد می کند:
الف) بسط مدل سلولی جهت استفاده برای الیاف مجاور
در این رویکرد حل معادله دو همساز (معادله (۴۲) نیاز به یک سری حل از مرتبه بالاتر از مدل سلولی ساده معادله (۴۳) نیاز دارد. مؤلفه های شعاعی پیوسته در حال تغییر است. این مؤلفه ها به سادگی نمیتوانند بوسیله شعاع سلولی و شعاع الیاف در مدل سلولی تعریف شوند. سنگانی (Sangani) و اکریووس(Acrivos) محققانی بودند که از این رویکرد استفاده کردهاند. آنها از متدلوژی خود برای تعیین یک حل عددی دقیق برای میدان جریان خزشی در ردیفهای با تخلخلهای زیاد و کم استفاده کردهاند.
کاهن (Kahn) براساس یک ارتباط شخصی که با مجید ضیا (Majid Zia) از دانشگاه رود ایسلند (Rhode Island) داشت، اعلام کرده است که ضیا حل سانگین و آکریووس را نسبت به حل کوابارا برای سرعت های در جهت جریان و شعاعی (در جهت شعاع) مقایسه کرده است و دریافت که وقتی سختی افزایش می یابد اختلاف بین این دو حل نیز افزایش می یابد، بویژه در نزدیکی نواحی مرزی سلولی نزدیک به ورودی جریان (upstream) و وقتی که فاصله از سطح الیاف بیشتر میشود این شرایط مشهودتر است. ضیا اشاره داشته است که درگ (drag) محاسبه شده برای سختی فیلتر تا ۴/۰ تقریبا یکسان است. اگر سختی بیشتر از ۴/۰ شود، اختلاف به سرعت افزایش می یابد. همچنین کاهن اظهار کرده است که برای ۲/۰≥χ افت فشار ناشی از نظم خطی (مدل کانالی در شکل۱) و متناوب سیلندرهای موازی تقریبا یکسان است، اما برای سختیهای بیشتر، درگ برای ردیفهای خطی بطور قابل ملاحظهای بیشتر از ساختمان متناوب است.
ب)روش های عددی
روشهای تفاضل محدود (finite difference methods) روشهایی هستند برای شکستن معادلات مشتق جزئی پیچیده در شبکه ای از معادلات همزمان (simultaneous equations). هر نقطه در شبکه برای تخمین حل تحلیلی، یکی پس از دیگری حل می شود. فردی (Fardi) و لیو (Liu) از این رویکرد برای حل مؤلفههای ساده شده معادلات ناویر استوکس در امتداد معادله پیوستگی برای سرعت سیال استفاده کردهاند. در صورتیکه شرایط مرزی مناسبی در سطح به کار برده شود، تحلیل های عددی نتایج خوبی را خواهند داشت.
پ)روش متغیر
اصل هلم هولتز برای یافتن الگوی جریان ناشی از پایینترین نرخ پراکندگی انرژی بوسیله درگ ویسکوزی استفاده میشود. تقارن پریودیک یا ترتیب الیاف با استفاده از سریهای فوریه (Fourier series) بکارگرفته میشود. براون با استفاده از مدل تغییراتی (variational model)، محاسباتی را انجام داده است و دریافت که اگر چه وقتی فواصل لیف- لیف و لایه- لایه با هم برابر هستند، افت فشار حساس به ترتیب الیاف نیست، ولی وقتی این دو فاصله با هم برابر نباشند، ساختمان رفتار بسیار متفاوتی خواهد داشت. اگر فاصله بین لایهها کمتر از فاصله بین الیاف باشد، آنگاه اثر تراکم میتواند شبیهسازی شود. علاوه بر این، بسته به اینکه لایههای متوالی دارای مدل کانالی باشند یا مدل متناوب، ساختمان رفتار متفاوتی خواهد داشت.
ت)روش المان مرزی
براون اشاره می کند به هیلدیارد (Hildyard) و همکارانش، محققانی هستند که از روش المان مرزی (boundary element method) استفاده کردهاند. در این روش، معادله دو همساز به دو روش چرخش ناشی از دو معادله انتگرالی، به دو معادله شکسته می شود. در این صورت، مسئله به حل همزمان معادلات کاهش می یابد. براون گزارش داده است که الگوهای جریان و افت فشار بدست آمده با استفاده از این مدل مشابه نتیجه حاصل از روش متغیر می باشد.
۵- تئوری مدل درگ
تئوری مدل درگ (drag model theory) بر اساس درگ یا کشیدن یک جسم متحرک از میان سیال میباشد. معادله درگ به صورت زیر است:
 به طوری که:
به طوری که:
F: نیروی درگ بر حسب N
p: چگالی سیال بر حسب kg/m۳
u: سرعت جسم متحرک در سیال بر حسب m/s
A: مساحت مرجع جسم بر حسب m۲
Cd: ضریب درگ (بی بعد)
اگر جسم، یک لیف باشد که به صورت یک واحد طول از یک سیلندر بلند عمود بر جریان در نظر گرفته شود،آنگاه :
(۶۱) F=1/2 pu۲dfcd
به طوریکه df عبارت است از قطر لیف بر حسب m.
توجه داشته باشید که در معاله (۶۱) مساحت مرجع A از معادله (۶۰) عبارت است از مقطع عرضی واحد طول سیلندر (واحد طول df).
با بکاربردن حل لامب (Lamb) برای یک لیف ایزوله شده :
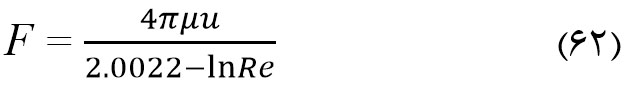 به طوریکهRe عدد رینولدز بوده و بصورت زیر تعریف می شود:
به طوریکهRe عدد رینولدز بوده و بصورت زیر تعریف می شود:
 ضریب درگ لمب برای معادله (۶۱) به صورت زیر است:
ضریب درگ لمب برای معادله (۶۱) به صورت زیر است:
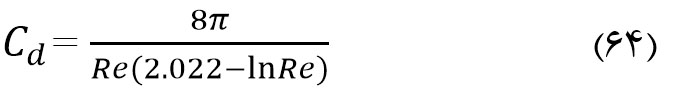 مشکل معادله لمب این است که این معادله برای یک لیف ایزوله است و اثرات تداخلی دیگر الیاف در همسایگی آن لیف در لایه فیلتر را در نظر نمی گیرد. بعضی از محققین مانند لانگمویر، ایروینگ، هپل و کوابارا موضوع بالا را با پرداختن به ساماندهی الیاف در داخل ترتیبهای موازی و قرار دادن یک بسته سلول سیال در اطراف هر لیف مورد بحث قرار دادهاند. دیگر محققان نظیر چن (Chen) با استفاده از الیاف مجاور مثل الیاف مرزی ضرایب درگ را تعیین کرده اند. چن فرض کرده است که در عدد رینولدز پایین (کوچک)، نسبت فاصله لیف- لیف (db) به قطر لیف (df) با ریشه دوم سفتی ( χ ) نسبت عکس دارد. پیش از آن محققی به نام وایت (White)، نشان داده است که ضریب درگ یک سیلندر متحرک در داخل یک منبع (تانک) میتواند با معادله زیر همبستگی داشته باشد:
مشکل معادله لمب این است که این معادله برای یک لیف ایزوله است و اثرات تداخلی دیگر الیاف در همسایگی آن لیف در لایه فیلتر را در نظر نمی گیرد. بعضی از محققین مانند لانگمویر، ایروینگ، هپل و کوابارا موضوع بالا را با پرداختن به ساماندهی الیاف در داخل ترتیبهای موازی و قرار دادن یک بسته سلول سیال در اطراف هر لیف مورد بحث قرار دادهاند. دیگر محققان نظیر چن (Chen) با استفاده از الیاف مجاور مثل الیاف مرزی ضرایب درگ را تعیین کرده اند. چن فرض کرده است که در عدد رینولدز پایین (کوچک)، نسبت فاصله لیف- لیف (db) به قطر لیف (df) با ریشه دوم سفتی ( χ ) نسبت عکس دارد. پیش از آن محققی به نام وایت (White)، نشان داده است که ضریب درگ یک سیلندر متحرک در داخل یک منبع (تانک) میتواند با معادله زیر همبستگی داشته باشد:
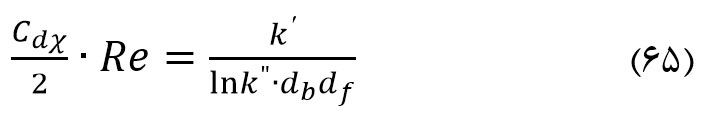 ‘K و “K ثابت های معادله فوق هستند.
‘K و “K ثابت های معادله فوق هستند.
چن معادله وایت (۶۵) را برای مدل خود مورد استفاده قرار داد. مدل چن یک توری متشکل از یک ماتریس مربعی از الیاف می باشد. فاصله داخل صفحه (in-plane) بین الیاف در جهت های x و y (طولی و عرضی) db بود. هر توری یک لایه مجزا را در فیلتر تشکیل می دهد.db به عنوان فاصله بین لایه ها نیز بود.
معادلات درگ حاصل از مدل چن به صورت زیر بودند:
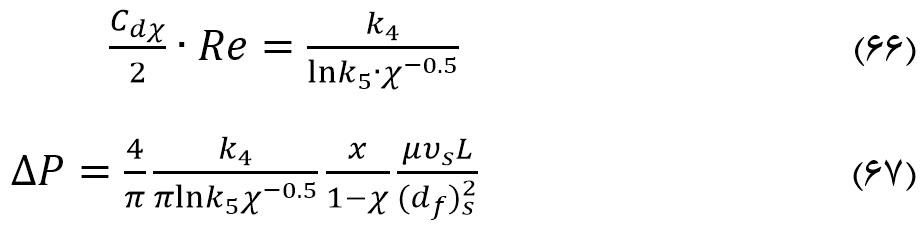 به طوریکه
به طوریکه
k۴ و k۵ : ثابت های معادله؛
PΔ: افت فشار در عرض فیلتر بر حسب Pa؛
μ: ویسکوزیته سیال بر حسب Pa/s ؛
υs: سرعت سطحی از میان فیلتر بر حسب m/s ؛
(df)s: قطر متوسط الیاف سطحی با واحد m.
تجربیات صورت گرفته توسط چن نشان می دهد که عبارت ضریب درگ یعنی Cdχ/۲∙Re در یک محدوده وسیعی از عددهای رینولدز(Re=۱۰-۳ تا Re=۱۰-۱)) ثابت است. همچنین چن داده های بهترین برازش را برای ثابت های k۴ و k۵ یعنی k۴=۰.۶۱ و k۵=۰.۶۴ تعیین کرده است.
خان (Khan) یک رویکرد مبتنی بر مدل توری ارائه کرده است که او آن را “مدل توری فرعی” (offset screen model) نامیده است. این مدل شامل دو لایه از الیاف موازی می باشد، الیاف سلولزی موجود در لایه اول عمود بر الیاف موجود در لایه دوم بودند. طرح این مدل در شکل ۲ به تصویر کشده شده است.هر لایه با مساحت ¯L × ¯L حاوی تعداد ¯N لیف با فاصله یکسان از یکدیگر در لایه اول و تعداد ¯M لیف با فاصله یکسان از یکدیگر در لایه دوم که عمود بر الیاف موجود در لایه اول هستند میباشد. خان یک پارامتر نا همگنی (anisotropy parameter) به صورت زیر تعریف کرده است:

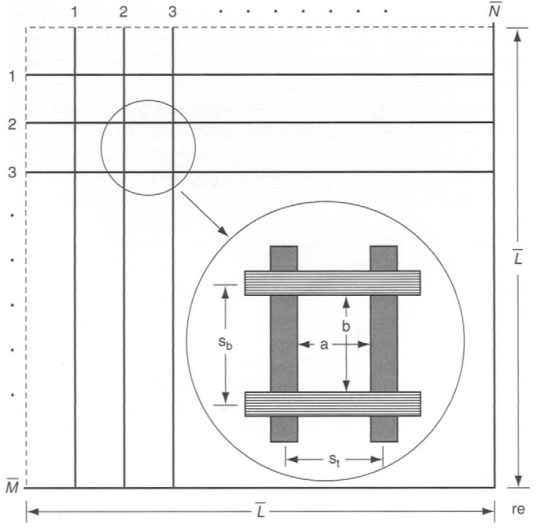
شکل۲- مدل توری فرعی خان
خان، پارامتر ناهمگنی را به آرایش یافتگی الیاف در لایه واقعی نسبت داد. او ادعا کرد که مدل او برای ویژگیهای ساختمانی مثل اندازه لیف، سفتی و ناهمگنی جواب می دهد. این مدل یک میدان جریان سه بعدی را نیز محاسبه کرده است. خان ثابت کرد که این مدل افت فشار را بسیار خوب پیش بینی کرد و اینکه به استثنای محیط هایی که در آنها انتشار، رهگیری و مکانیزمهای اینرسی دارای اهمیت یکسان بودند، راندمانهای به دام انداختن ذره به خوبی با دادههای تجربی قابل مقایسه است. او همچنین نشان داد که ناهمگنی فقط برای سفتی های بیشتر از ۲/۰ بر روی افت فشار تاثیر دارد.
۶- دینامیک سیال محاسباتی (computational fluid dynamics)
ظهور کامپیوتر و دسترسی روز افزون ابزارهای نرم افزاری محاسباتی، دانشمندان در حوزه فیلتر را قادر ساخته است تا راههای پیشرفتهای را برای فرآیند فیلتراسیون بیابند. یک چنین ابزاری که به دینامیک سیالات محاسباتی یا CFD معروف است، به تدریج در حال تبدیل شدن به یک ابزار مهم در طراحی و مدلینگ سیستمهای فیلتراسیون میباشد. دینامیک سیالات محاسباتی یا CFD، یک ابزار نرم افزاری است که میتواند برای شبیه سازی دینامیک جریان سیال در شرایط مختلف شامل جریان از میان لایه های متخلخل، مورد استفاده قرار گیرد. شبیه سازی در این ابزارهای نرم افزاری با حل معادلات ناویر- استوکس برای بقای جرم ،گشتاور و انرژی یک سیال انجام می شود. این معادلات معادلات دیفرانسیلی هستند که میتوانند با فرمولاسیون گسسته (discrete formulation) که در حجمهای محدود و ترجیحا حجمهای بسیار کوچک حل میشوند، تخمین زده شوند. از آنجا که در این روش از تخمین استفاده می شود، اغلب ضروری است که از روش های تجربی برای پدیدههایی استفاده شود که به اندازه کافی برای سطح معینی از گسسته سازی حل نمیشوند. اثرات اغتشاش سیال و لایه های متخلخل دو مقادیری هستند که می توانند به کمک CFD مدل شوند.
مقالات فراوانی در استفاده از CFD برای کاربردهای مختلف فیلترها وجود دارد بعضی از این مقالات عبارت اند از:
۱- Application of computational fluid dynamics to air induction system design” Chen et al. ” یک متدلوژی برای به کارگیری ابزارهای CFD برای تجزیه و تحلیل سیستمهای فیلتراسیون و القای هوا در اتومبیل ارائه میدهند.
۲- “Simulating the deep-bed loading and soot cake growth in a DPF Using a 3-D CFD model” Yi and Egalia- یک مدل CFD سه بعدی مفصل عملیات جریان و فیلتراسیون دود را در فیلترهای جداکننده ذرات در خودروهای دیزلی شبیهسازی میکند.
۳- “Numerical analysis of air filtration and pulse jet cleaning in a dust collector” Lo et al.- روش CFD برای سنجش تغییرات فشار در عرض کارتریج های فیلتر پلیسه ای (آلکاردئونی) در تمیز کردن بوسیله جت در جمعکننده (کلکتور) گردوغبار استفاده میشود.